Reflection Rules How To W 25 Step By Step Examples
Reflection over y=x Share Video https//wwwshowmecom/sh/?h=d5WHhqa The reflection of the point (x, y) across the xaxis is the point (x, y) P(x,y)→P'(x,y) or r xaxis (x,y) = (x,y) Hint If you forget the rules for reflections when graphing, simply fold your graph paper along the line of reflection (in this example the xaxis) to see where your new figure will be located Or you can measure how far your
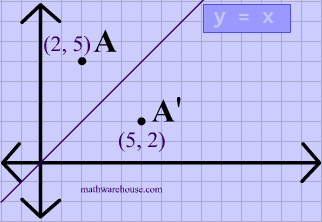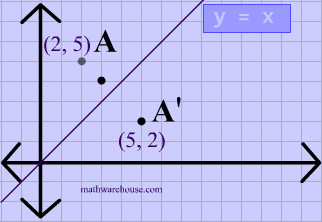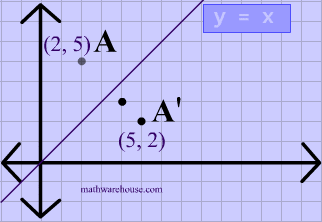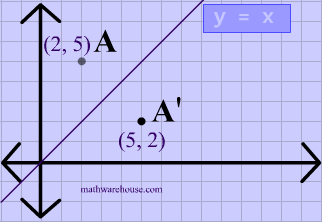
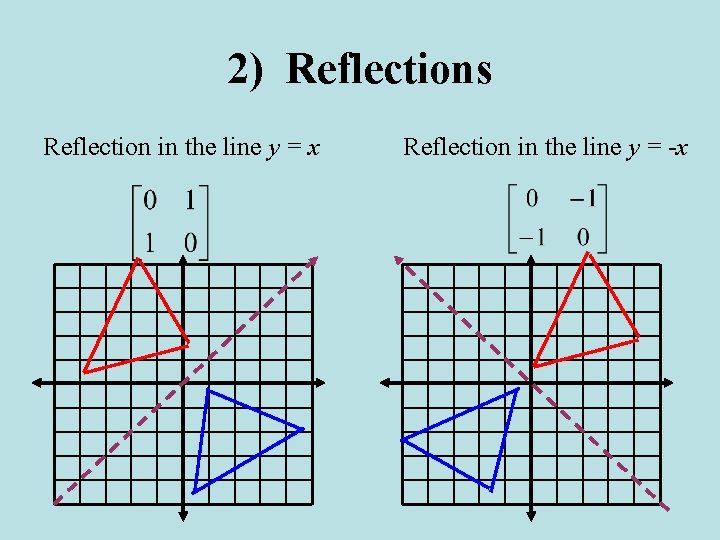
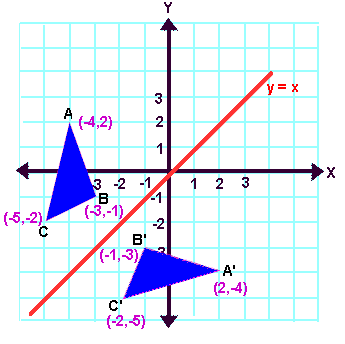
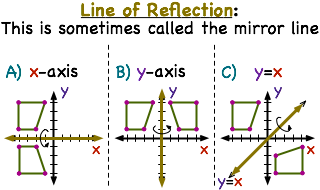
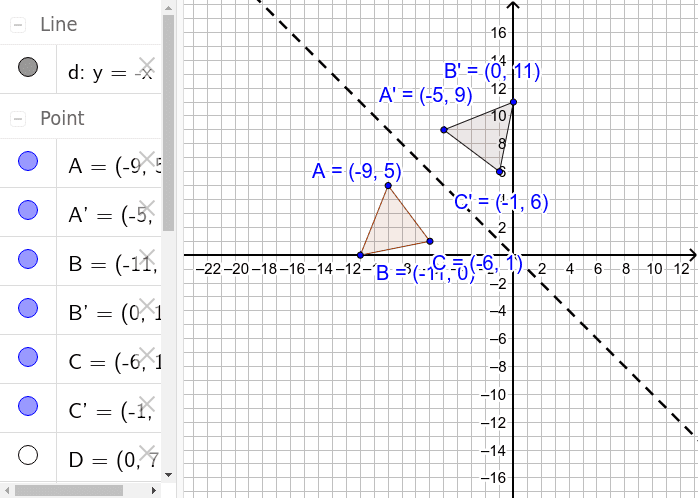
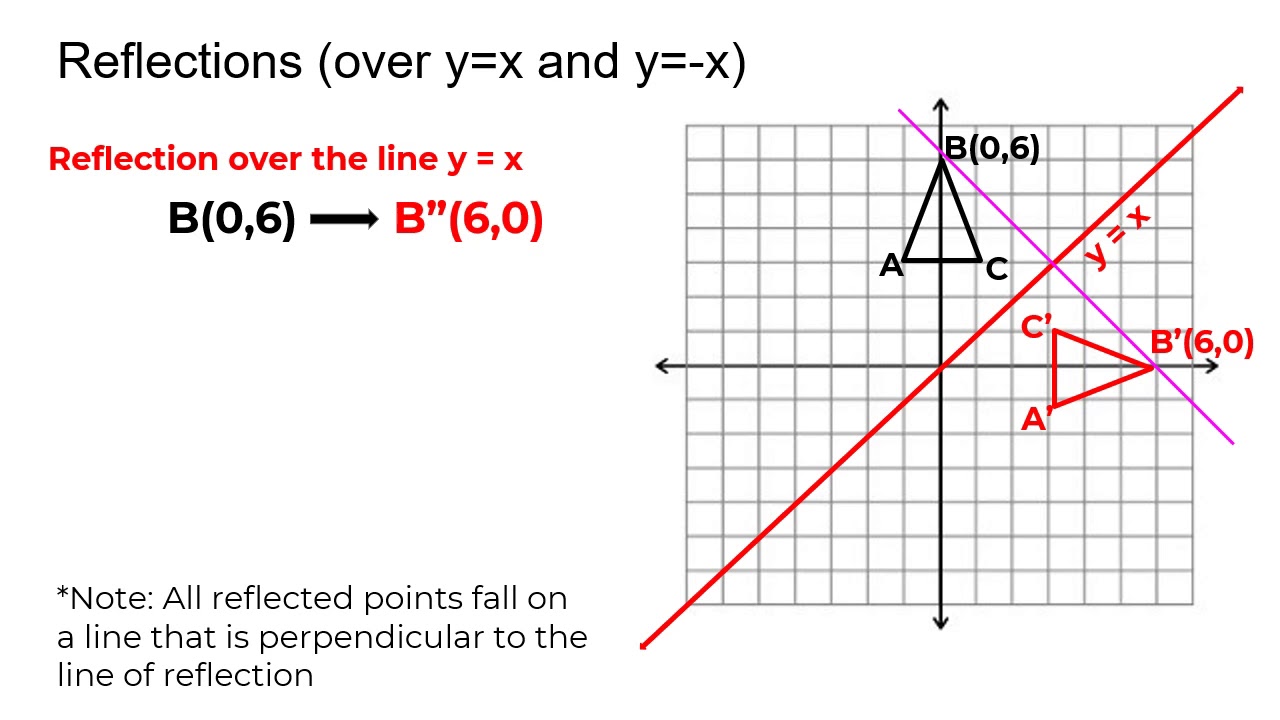
Y=x reflection line
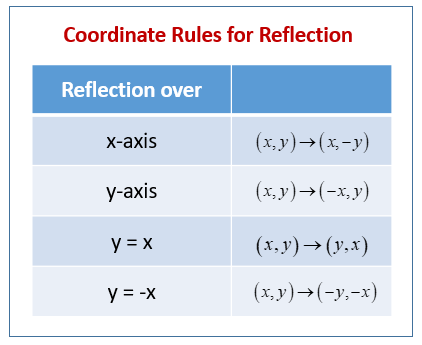
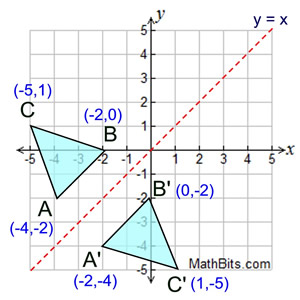
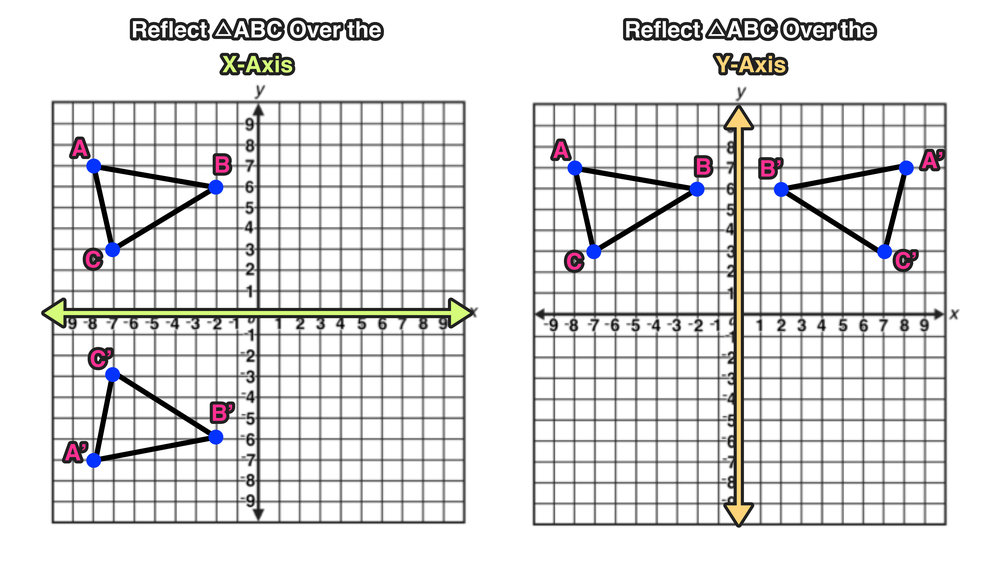
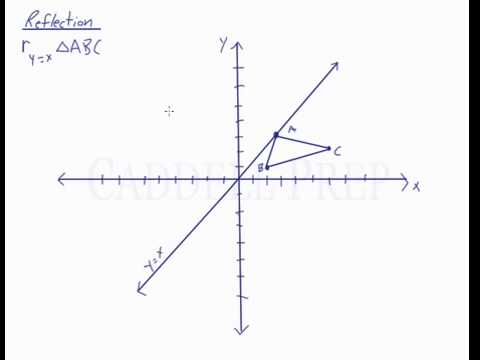
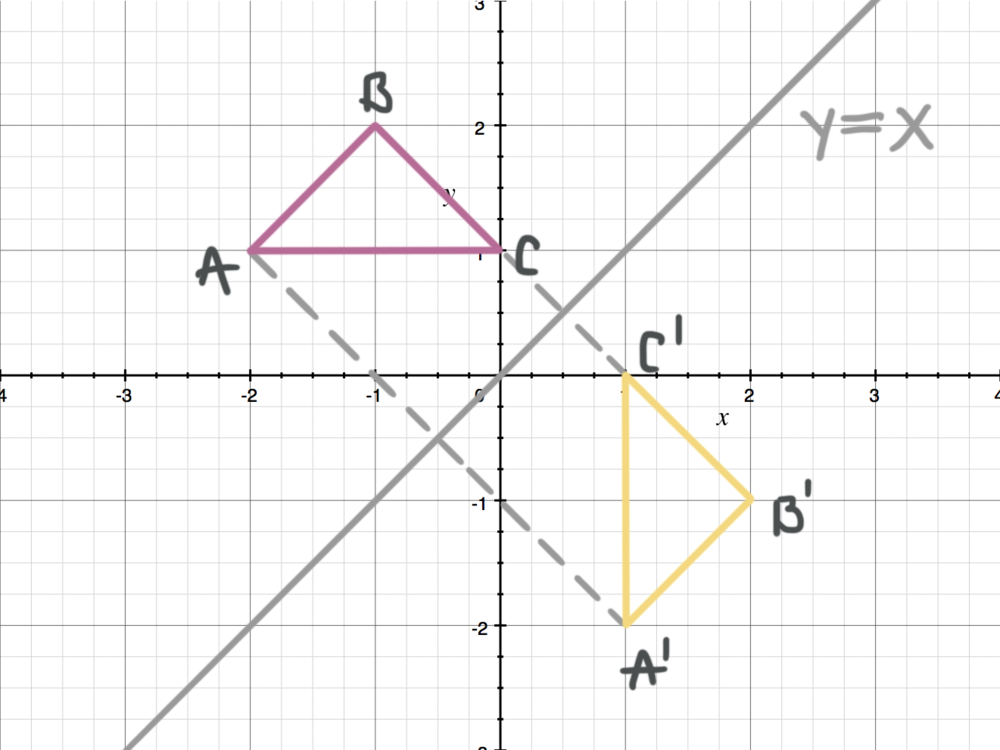
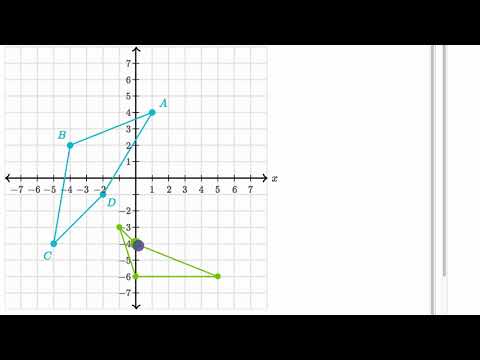
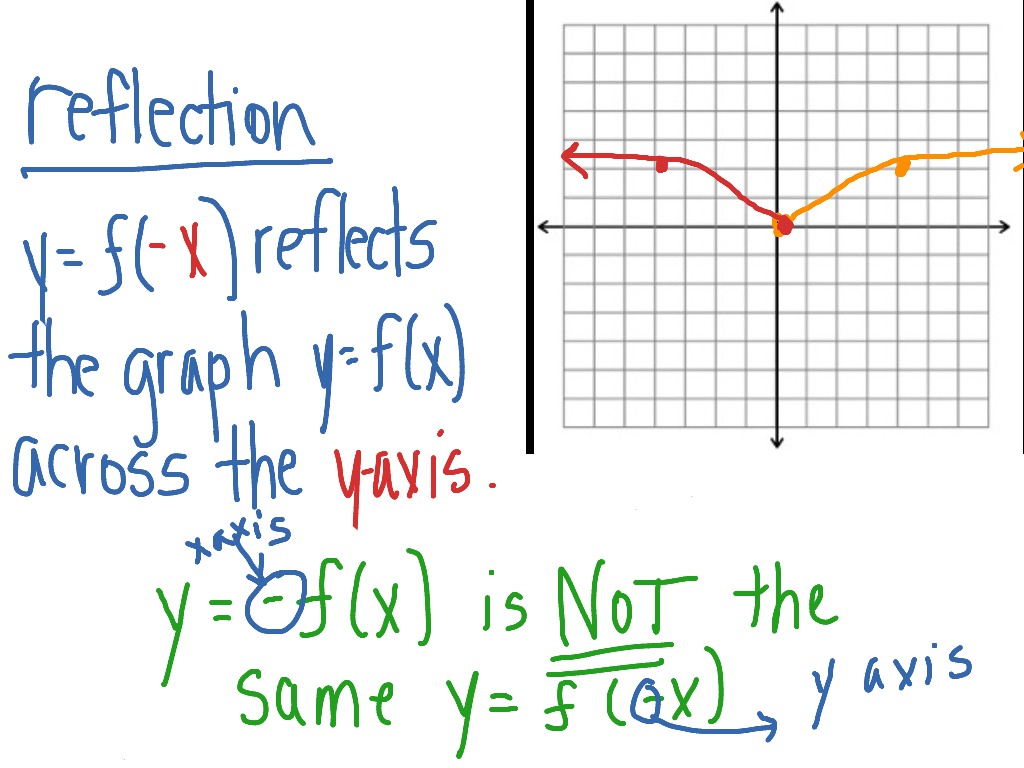
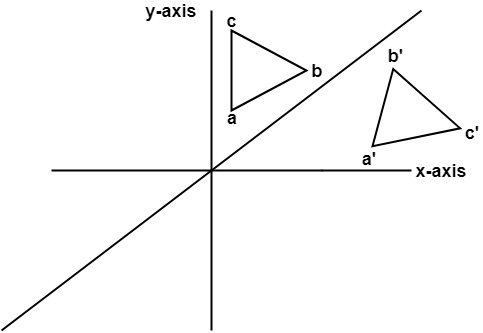
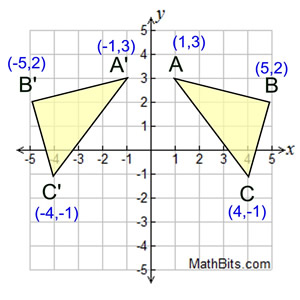
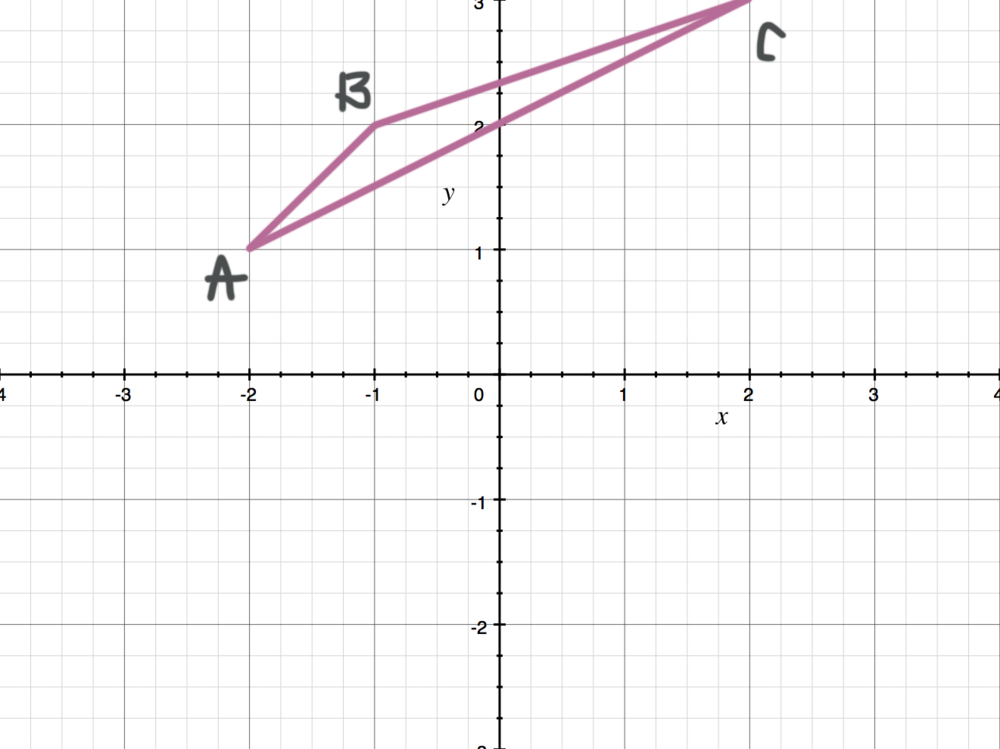
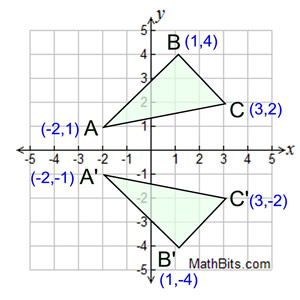
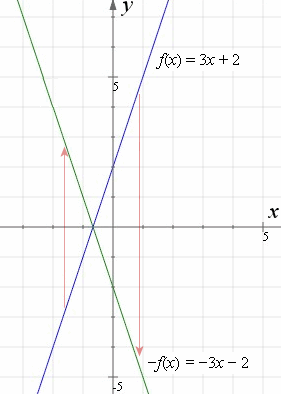
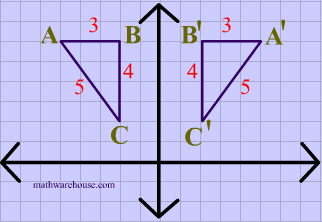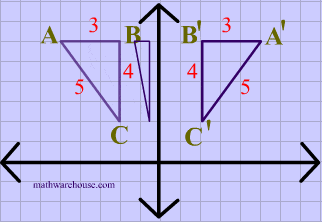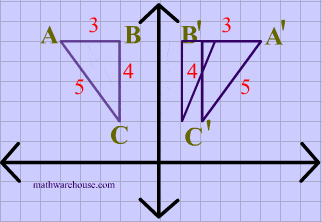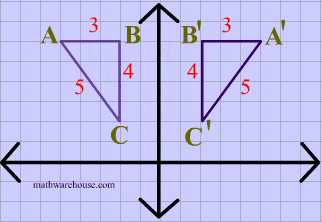
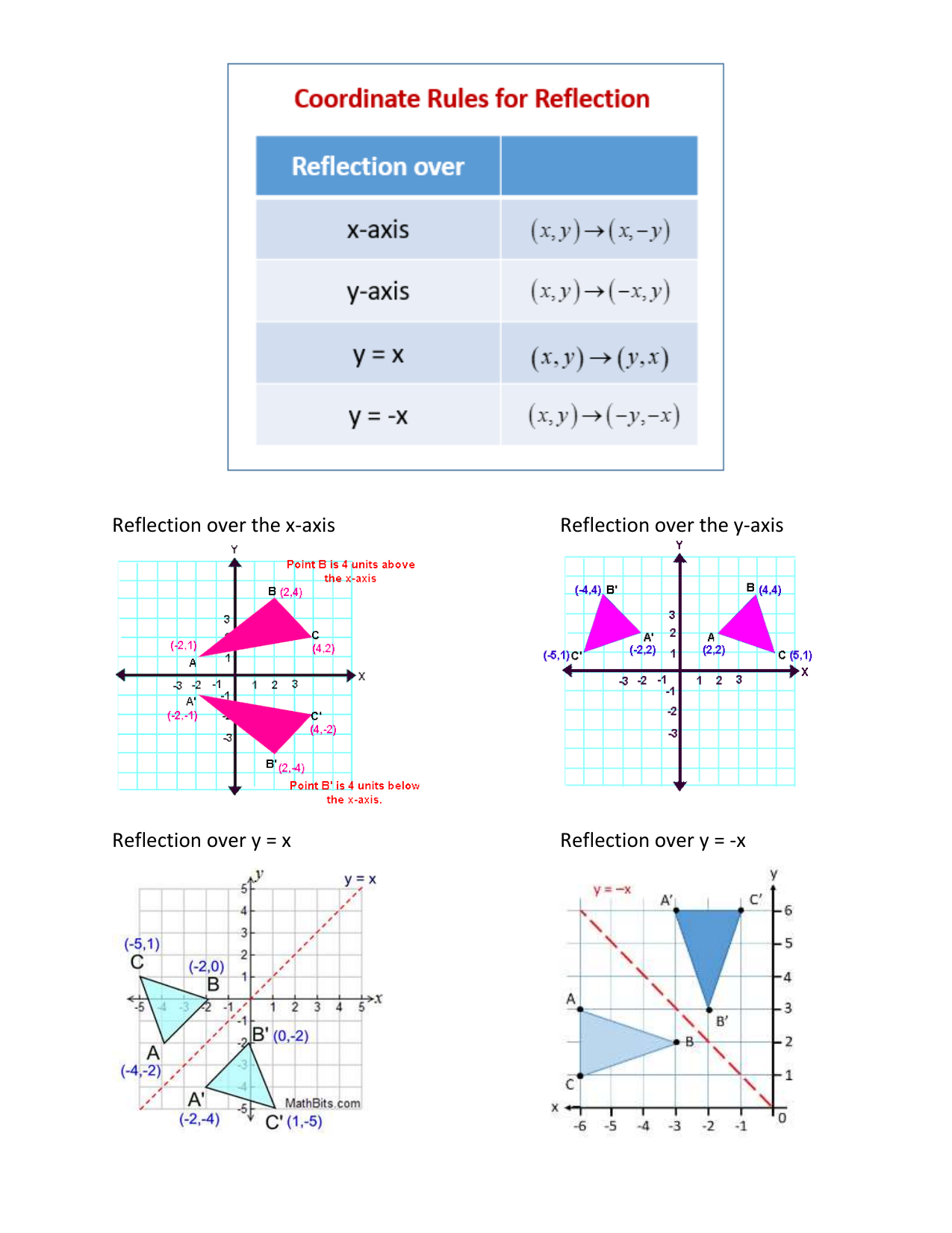
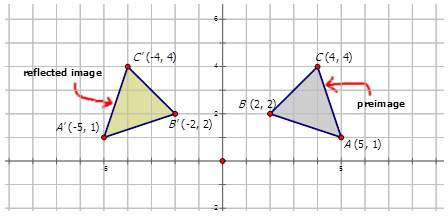
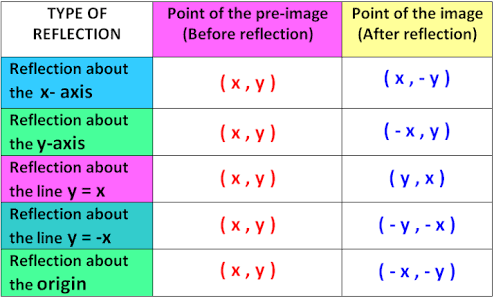
Y=x reflection line-Here the original is ABC and the reflected image is A'B'C' Some Tricks XAxis When the mirror line is the xaxis we change each (x,y) into (x,−y) YAxis When the mirror line is the yaxis we change each (x,y) into (−x,y) Fold the Paper And when all else fails, just fold the sheet of paper along the mirror line and then hold it up to theA math reflection flips a graph over the yaxis, and is of the form y = f (x) Other important transformations include vertical shifts, horizontal shifts and horizontal compression Let's talk about reflections Now recall how to reflect the graph y=f of x across the x axis
Reflection Over A Line Expii
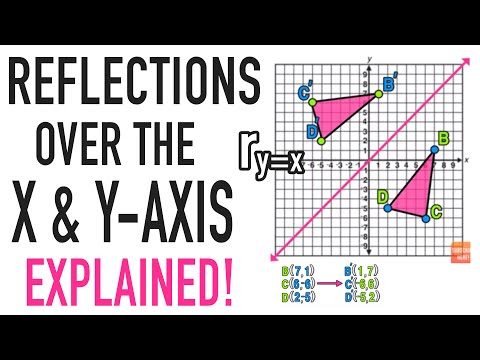
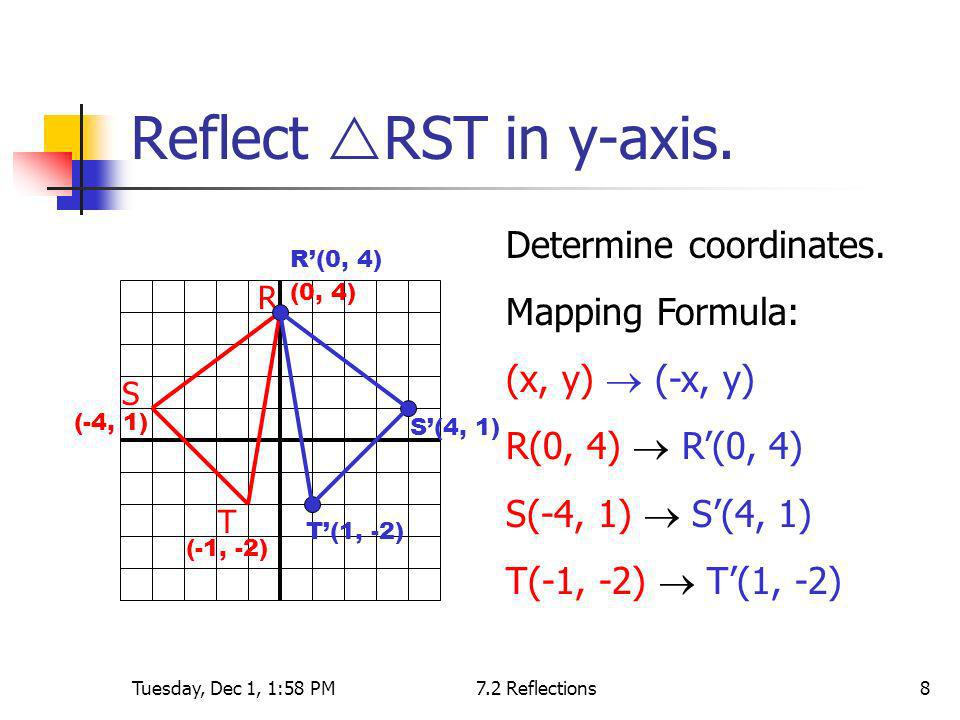
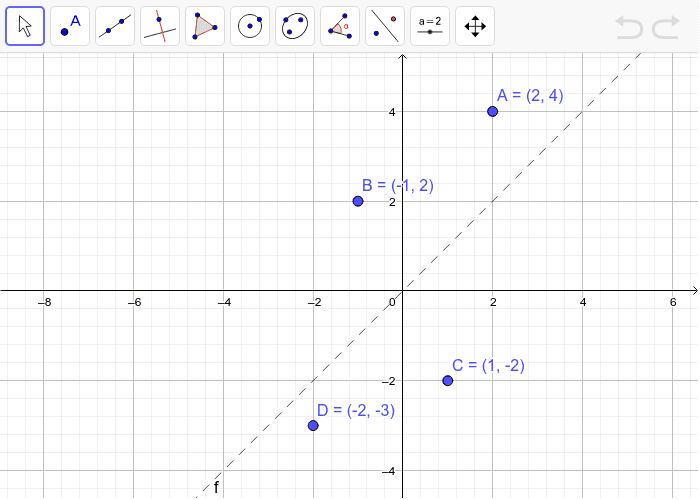
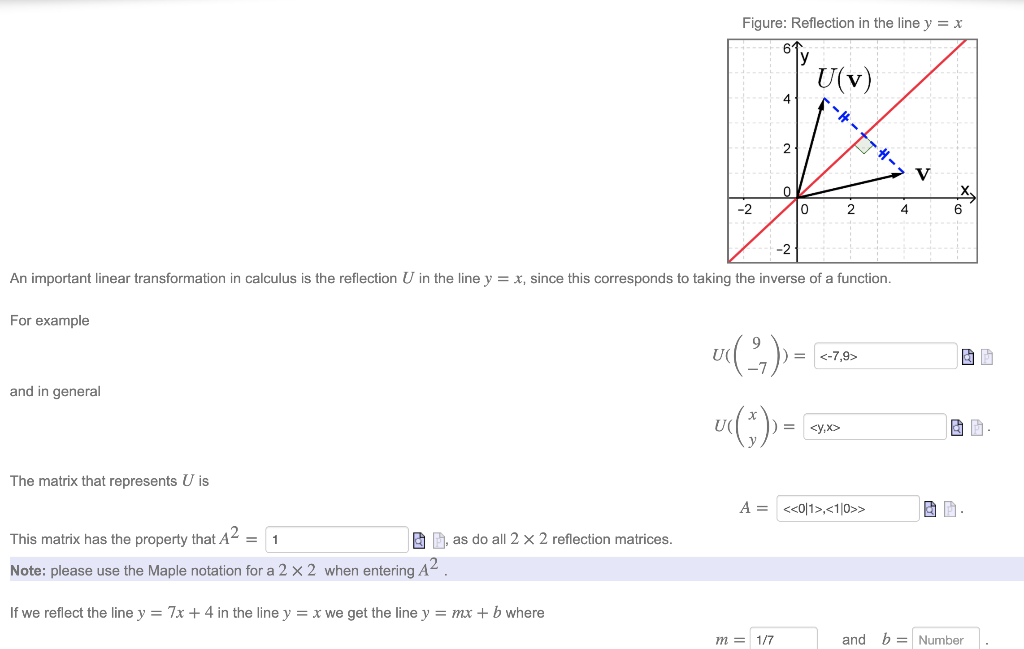
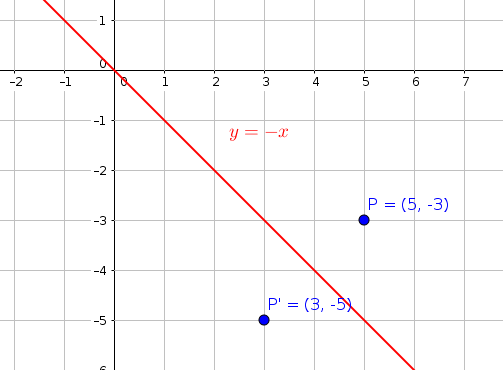
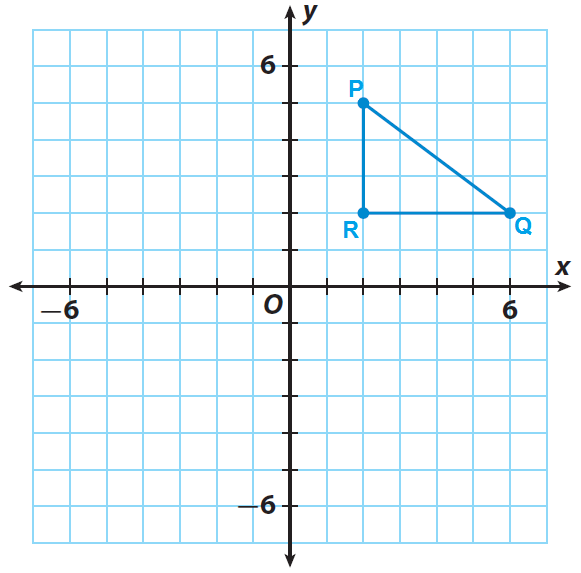
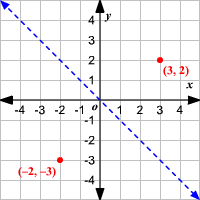
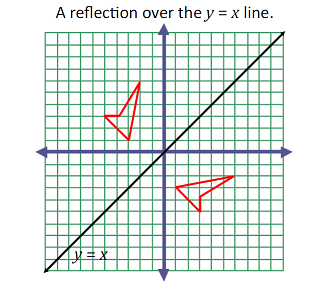
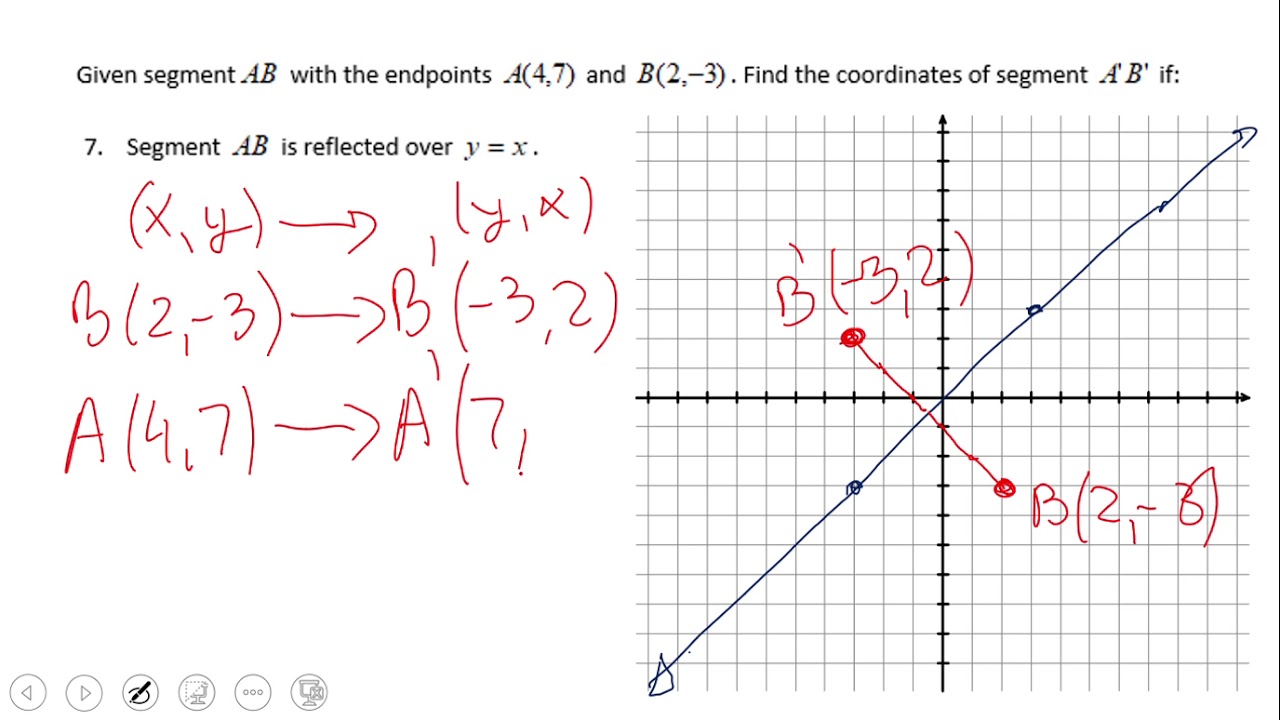
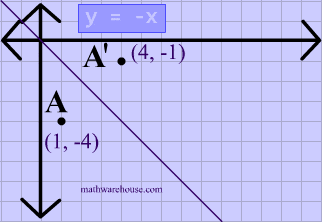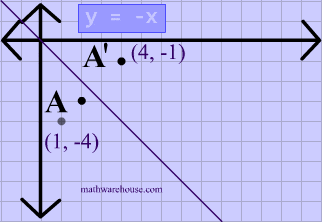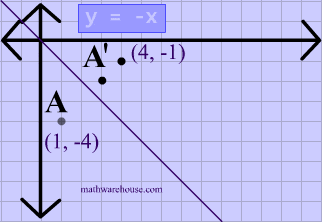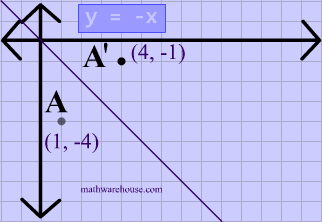
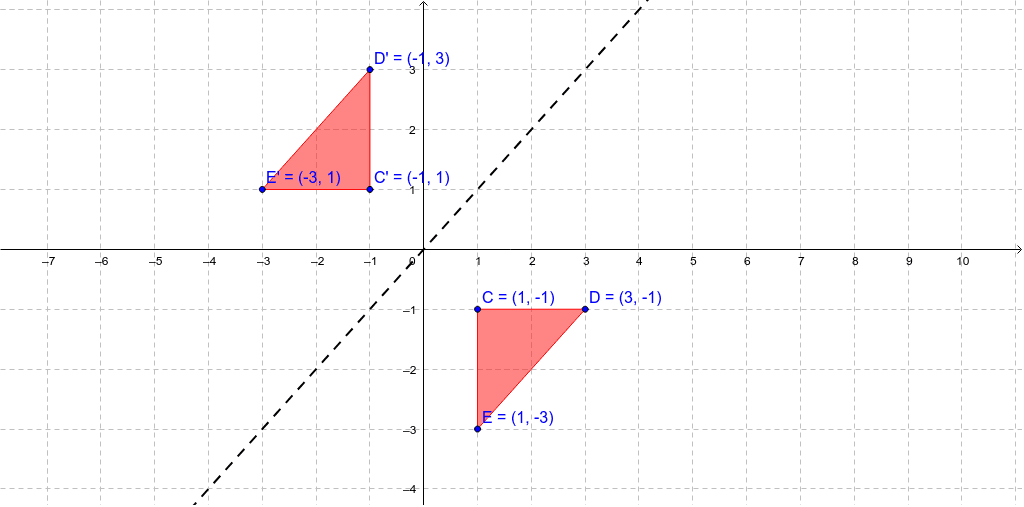
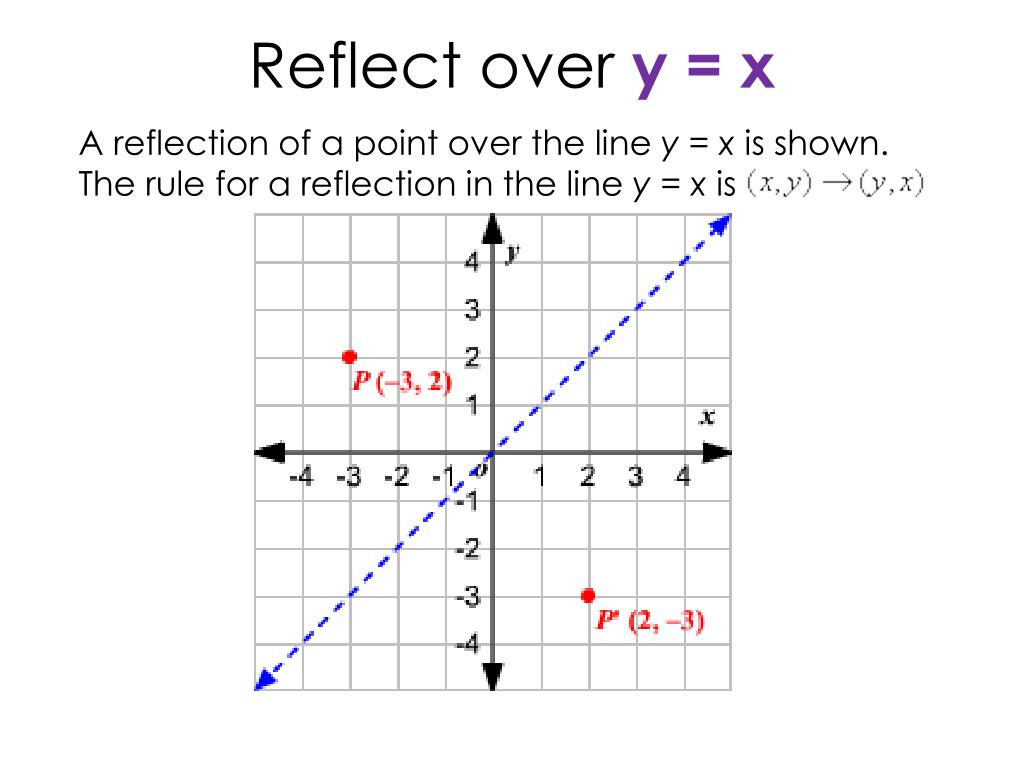
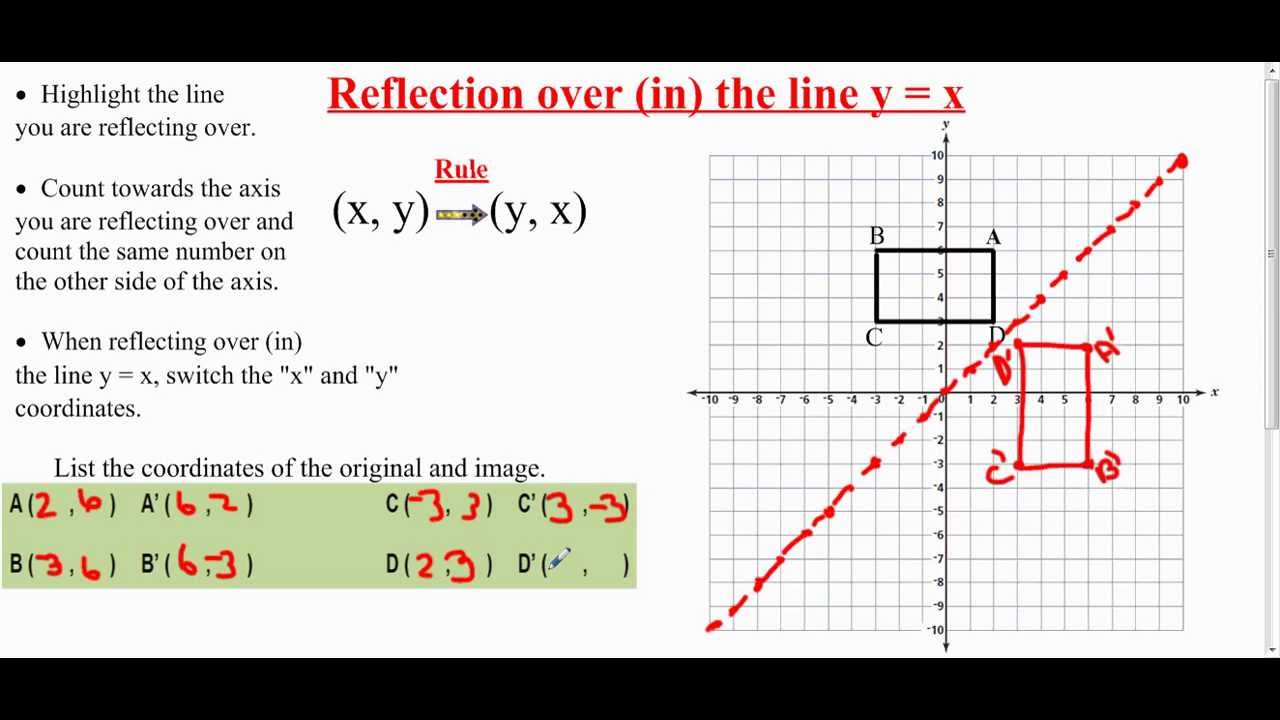
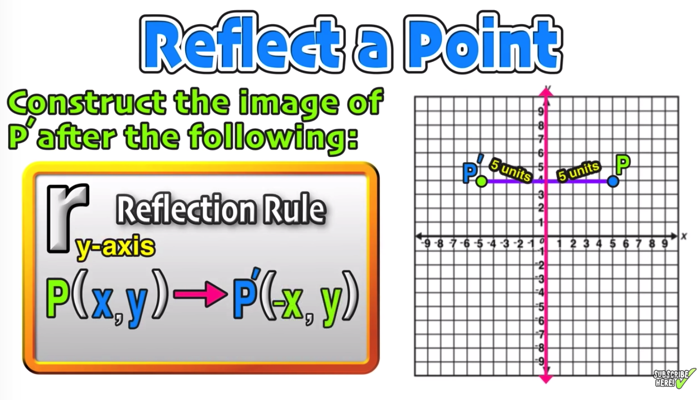
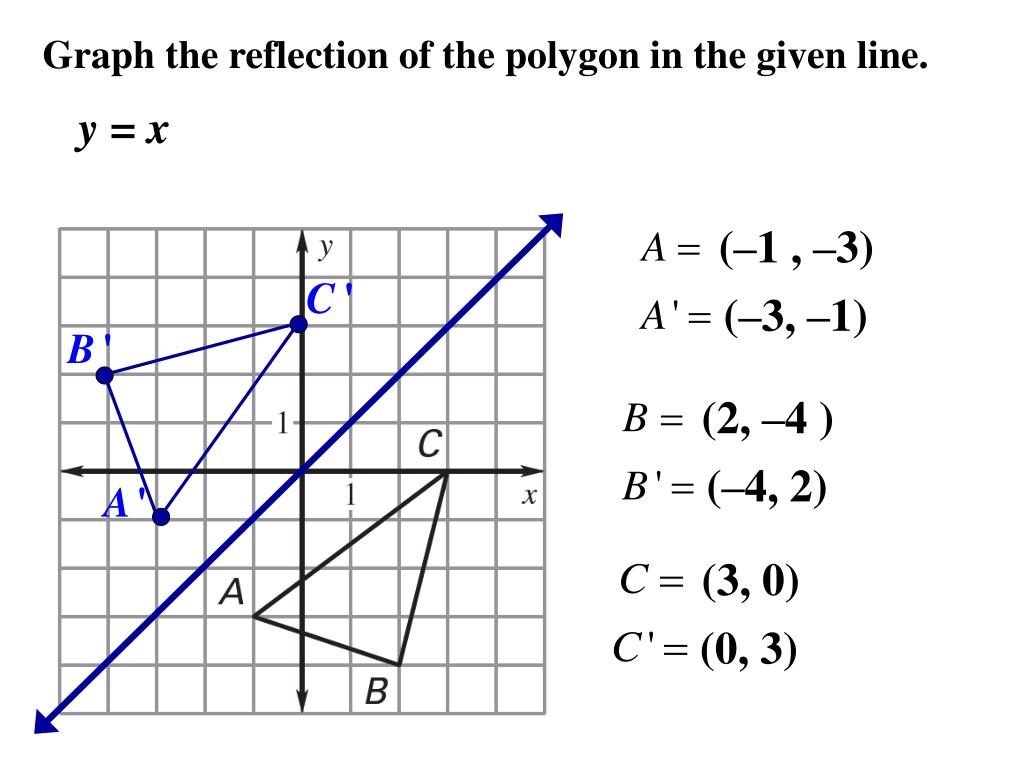
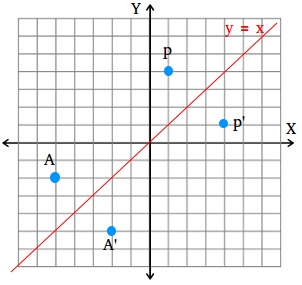
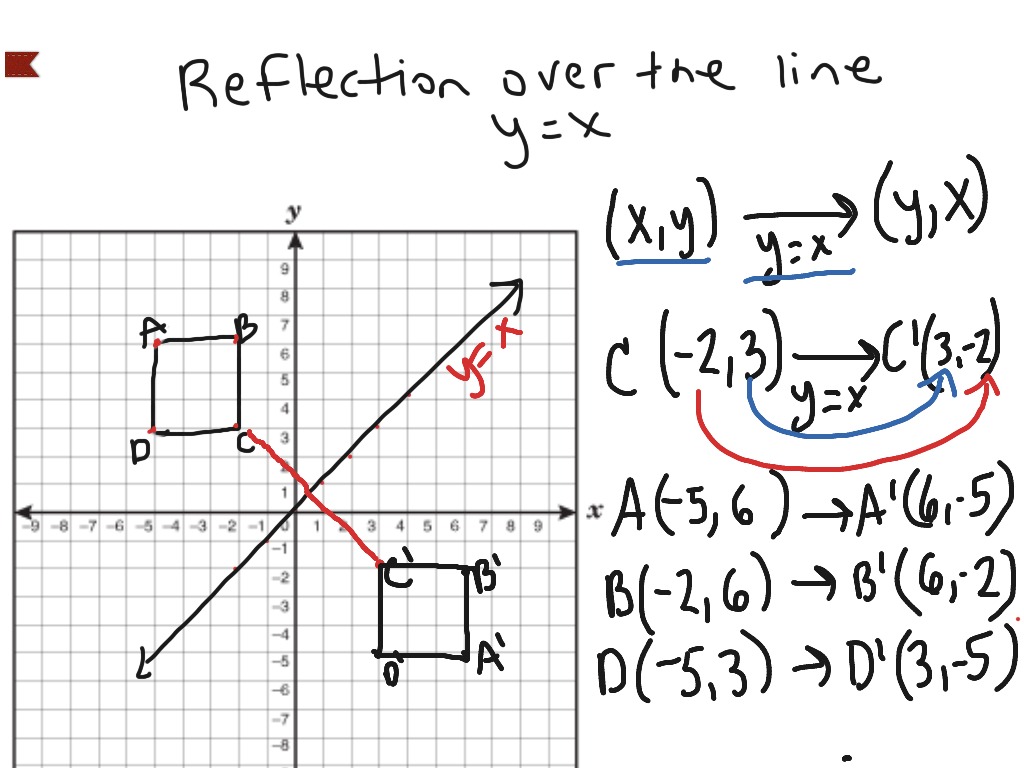
Reflect over the y = x When you reflect a point across the line y = x, the xcoordinate and ycoordinate change places If you reflect over the line y = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed) $(x, y) → (x, y)$ Other Horizontal and Vertical Lines The easiest way to do a reflection about another horizontal or vertical line is to Draw the line;The rule for reflecting over the Y axis is to negate the value of the xcoordinate of each point, but leave the value the same For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)
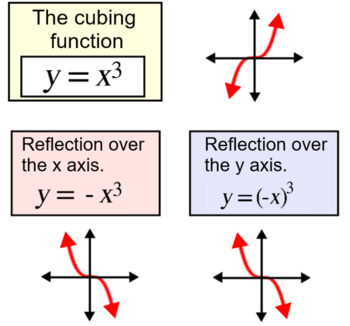
Y = f (x) The graph of y = f (x) can be obtained by reflecting the graph of y = f (x) through the yaxis It can be done by using the rule given below That is, if each point of the preimage is (x, y), then each point of the image after reflection over yaxis will be (x, y) Example Do the following transformation to the function y = √xDescribe the Transformation y=x^3 The parent function is the simplest form of the type of function given For a better explanation, The graph is reflected about the yaxis when Reflection about the yaxis None Compressing and stretching depends on the value of When is greater thanConsider the line and original object as one figure Translate the entire figure to the line of reflection maps to the xaxis (for horizontal lines) or yaxis (for vertical lines) Reflect
Y=x reflection lineのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | 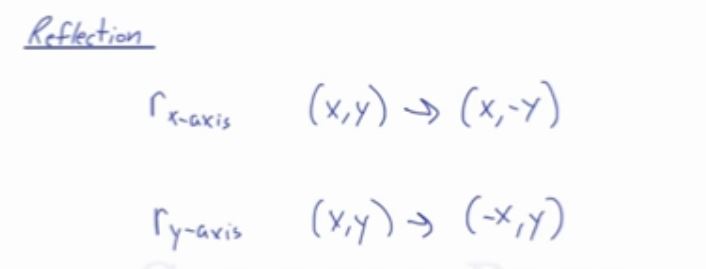 |  |
 |  | 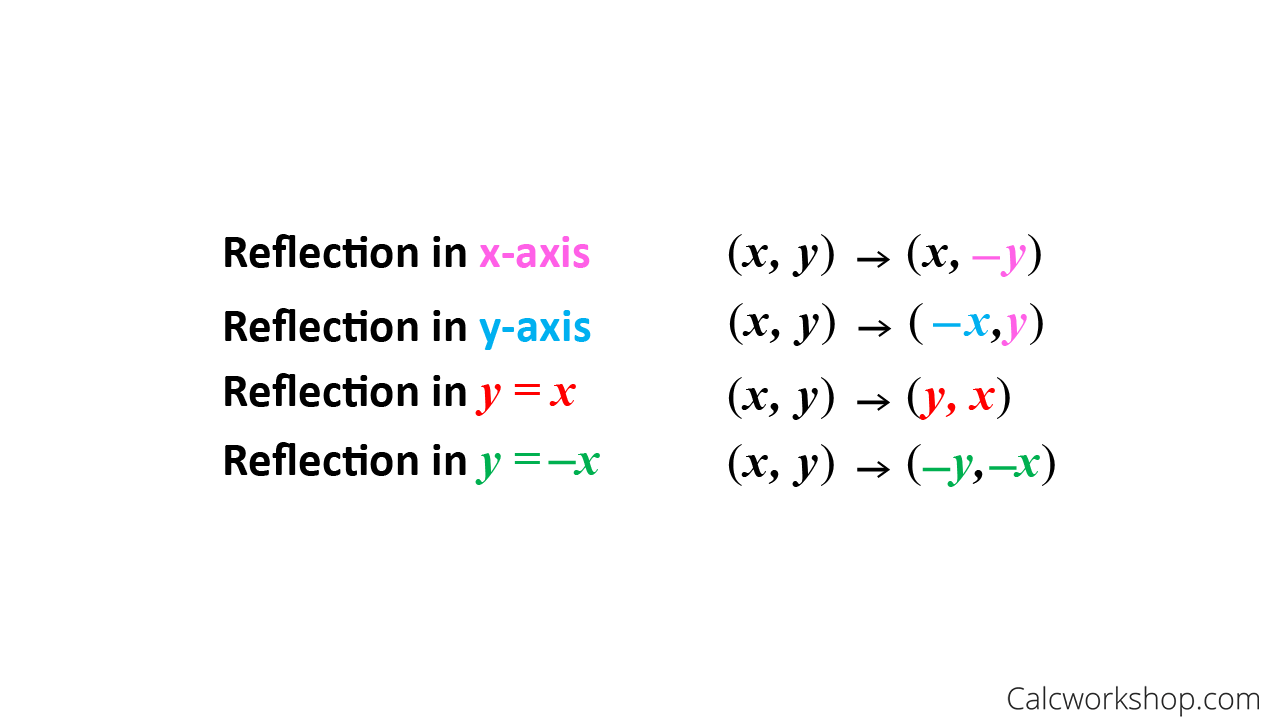 |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 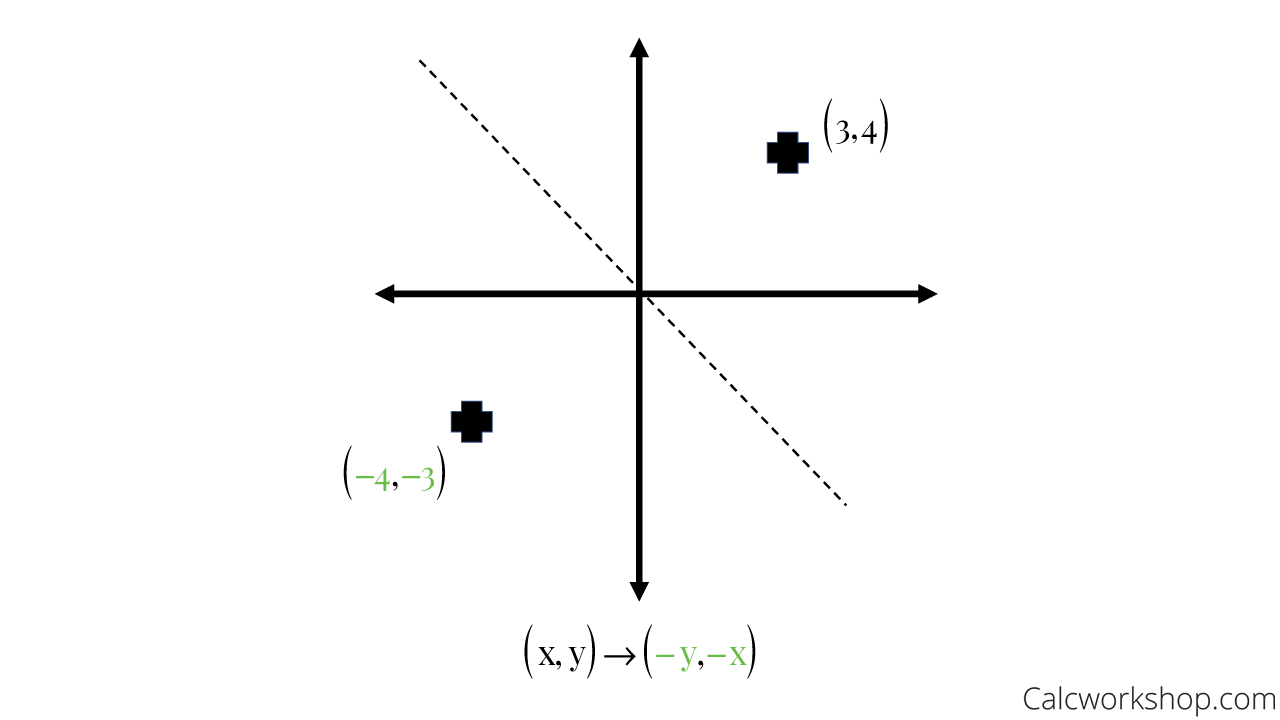 | |
 |  |  |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=x reflection line」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
Graphing Reflections of latexf\left(x\right)={\mathrm{log}}_{b}\left(x\right)/latex When the parent function latexf\left(x\right)={\mathrm{log}}_{b}\left(x\right)/latex is multiplied by –1, the result is a reflection about the xaxis When the input is multiplied by –1, the result is a reflection about the yaxis Sets of Coordinates (x, y), Functions, Coordinates (with Matrices) 1 Reflection Over The XAxis Sets of Coordinates If you have a set of coordinates, place a negative sign in front of the value of each yvalue, but leave the yvalue the same Example question #1 Reflect the following set of coordinates over the xaxis
Incoming Term: y=x reflection, y=x reflection calculator, y=x reflection matrix, y=x reflection example, y=x reflection equation, y=x reflection line, y=x reflection translation, y=-f(x) reflection, y=-x graph reflection, y=x axis reflection,




0 件のコメント:
コメントを投稿